Senior Projects 2021
Claire Bordenave - The Impact of Online and Hybrid Learning, Advisor Dr. Carla Gerberry
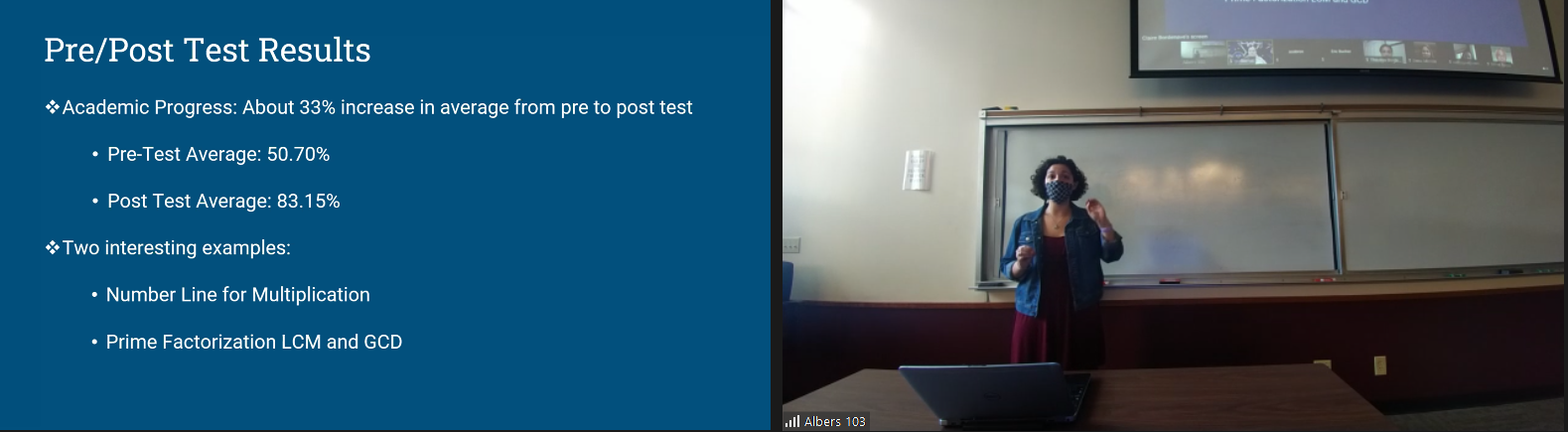
Technology has become increasingly integrated in schools, and the COVID-19 pandemic forced the rapid adaptation of online classrooms. With this new educational model being so heavily implemented, this study set out to determine the impact of online and hybrid schooling. We surveyed 3 sections of a mathematics number theory course geared for undergraduate early childhood majors. The surveys were tailored to gage the students’ self-efficacy and overall sentiment in regard to the online course, while pre and post tests were given to gage academic performance. At the end of the semester, most students were pleased with their grades in the course and felt relatively confident in the material. Additionally, there was about a 33% increase in the pre to post test average. In the end, it was concluded that online and hybrid learning can be an effective learning model, depending upon the organization of the instructor and the commitment of the student.
Amanda Cusimano - Linear Bandwidth of Binary Trees, Advisor Dr. Eric Bucher
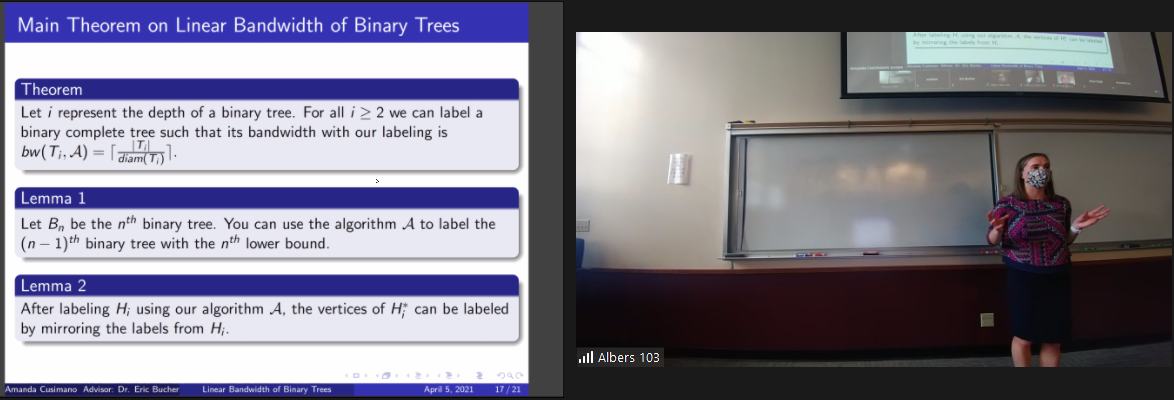
Graphs and their linear embeddings can be used to model real world problems related to anything from network traffic to maximum flow in supply chains. In this talk, we will define the linear bandwidth of a graph using various examples. We will then focus on complete binary trees and the properties of these trees that make finding their linear bandwidth a unique problem. Our main theorem includes an explanation of the lower bound for the bandwidth of complete binary trees as well as a labeling algorithm that produces an embedding with bandwidth equal to the lower bound. This talk will be accessible for all math majors.
Kelly DeLano - Modeling the Transmission of COVID-19 in Relation to Behavioral Response, Advisor Dr. David Gerberry
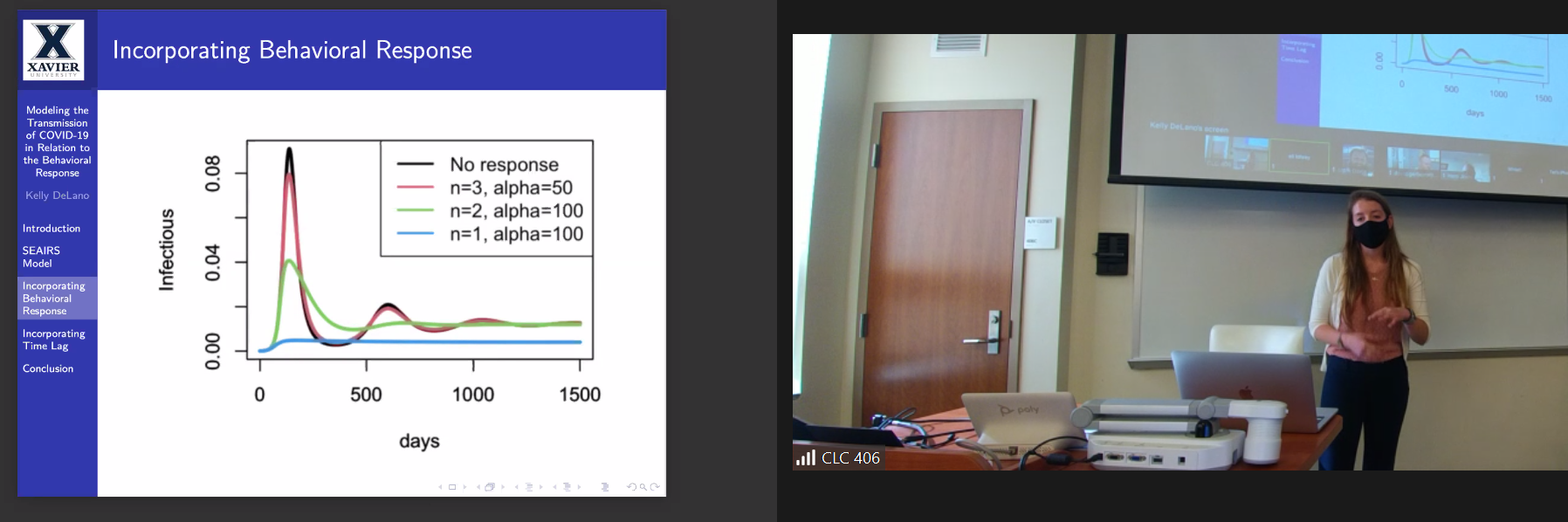
This project analyzes the spread of the COVID-19 virus throughout a population. We created an SEAIRS model to quantify the number of susceptible, exposed, asymptomatic, infectious, and recovered people in the population. After creating a general model, we incorporated behavioral response where the population acts to reduce transmission as the pandemic becomes more severe. Next, we recognized that the prevalence on one specific day doesn’t impact the behavioral response on that day, and instead a few days later, so we implemented a “lag function.” With these assumptions the mathematical model produces the multi-peak behavior that has characterized the COVID pandemic.
Sophia Fahey - Sign Patterns that Require or All Hn, Advisor Dr. Minnie Catral
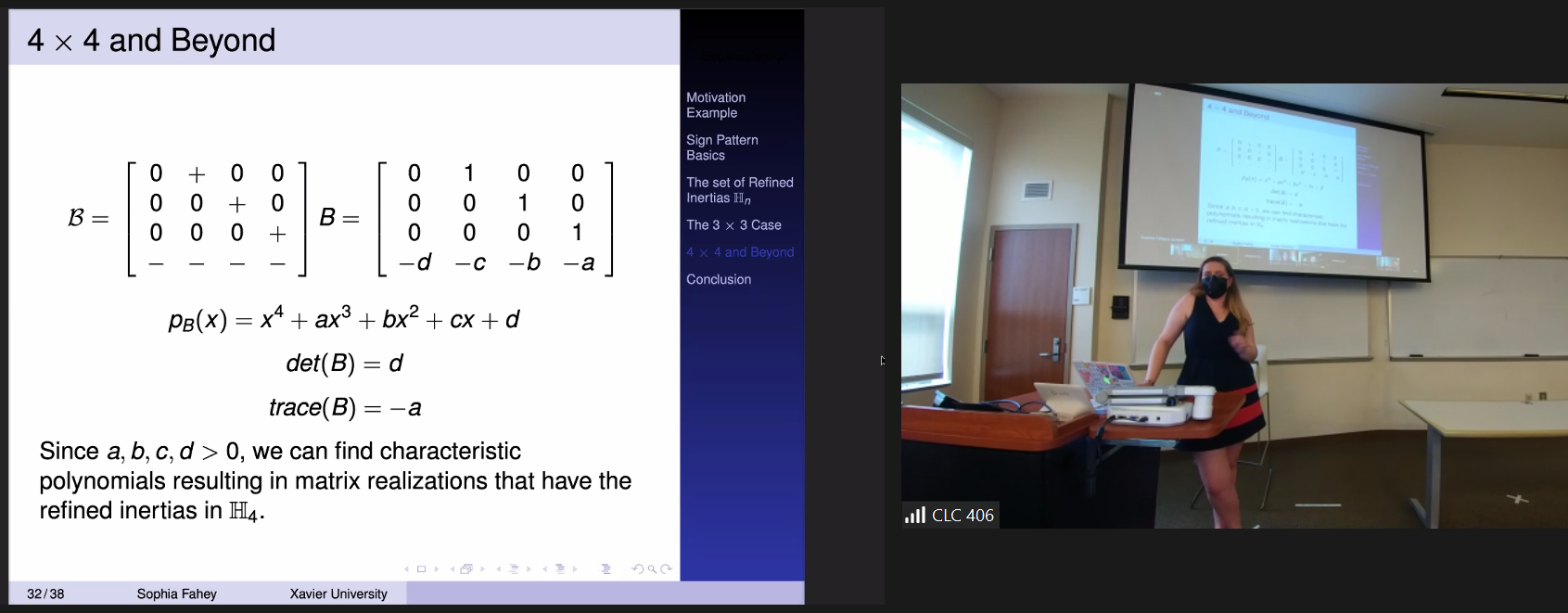
Sign pattern matrices arise naturally in fields such as economics, biology, sociology and more. A sign pattern matrix is a matrix whose entries are either +, - , or 0. In some applications, these entries are dependent on the signs of coefficients in a system of equations making them useful in analyzing the stability of that system. The refined inertia of a matrix is an ordered 4-tuple of nonnegative integers giving the number of eigenvalues with positive real part, the number of eigenvalues with negative part, the number of zero eigenvalues, and the number of purely imaginary eigenvalues. The refined inertia of a sign pattern is the set of all possible refined inertias over all matrices that has that sign pattern. This presentation focuses on a specific set of refined inertias for an n x n sign pattern namely {(0,n,0,0),(2,n-2,0,0),(0,n-2,0,2)}. Such patterns are related to Hopf bifurcations in dynamical systems.
Emma Hiatt - The Distance Spectra of Graphs, Advisor Dr. Minnie Catral

Given a graph, we can associate a matrix by assigning each pair vertices a value that corresponds to an entry in the matrix. The most well-known and researched matrices are the Adjacency and Laplacian. Other matrices such as the Distance Matrix are less studied. We focus on associating the Distance Matrix to different families of graphs. Then we use techniques from Linear Algebra to perform an analysis on relationships discovered with respect to their characteristic polynomials, eigenvalues, and spectrum. The discovery of these relationships offer insight to structural properties of graphs.
Amy Kucera - The Linear Bandwidth of Cyclic Caterpillars, Advisor Dr. Esmeralda Nastase
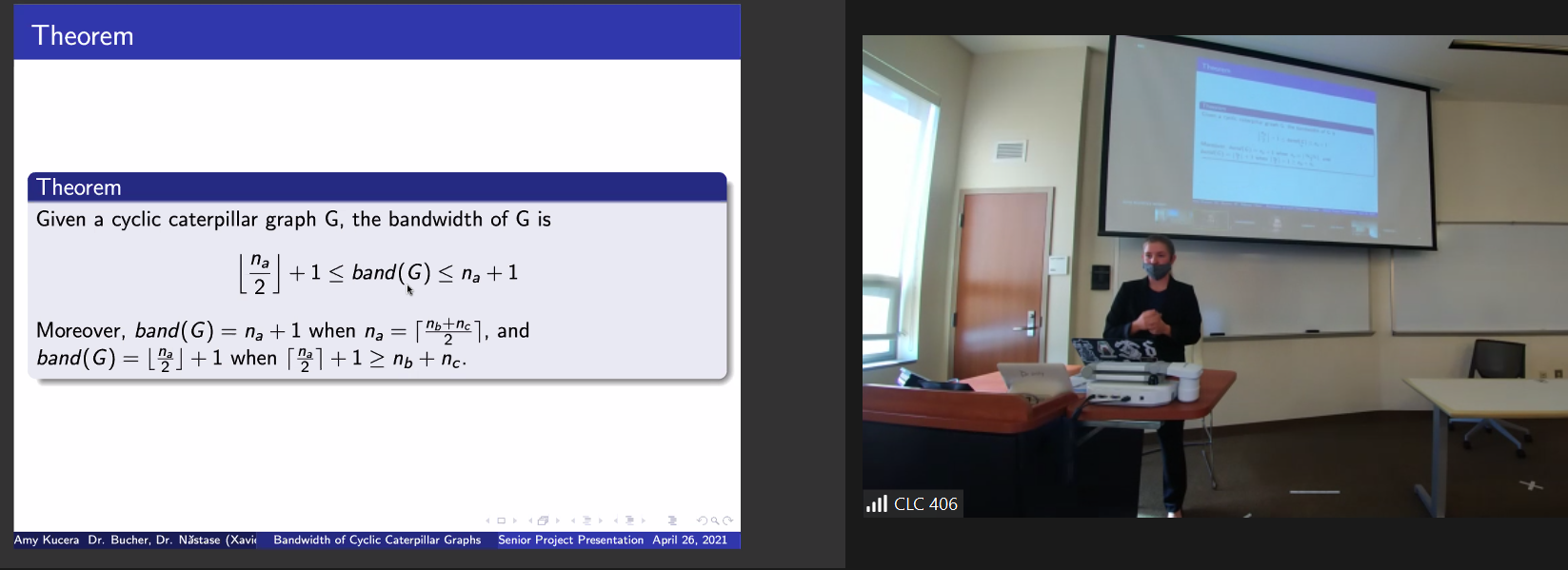
The graph bandwidth problem can be thought of as placing the vertices of a graph at distinct integer points along the x-axis so that the length of the longest edge is minimized. Such placement is called a linear embedding of the graph, and the minimum of all possible embeddings is called the bandwidth of the graph. In this talk, I will explore the properties of linear bandwidth of cyclic caterpillar graphs and how the distribution of pendants attached to the vertices of the cycle affect the bandwidth.
Rachel Osborne - Monopoly as a Markov Process, Advisor Dr. David Gerberry

Monopoly is a household favorite board game, but it also can be viewed as a random process with a Markov property. In this presentation, we examine this well-known game as a Markov process, looking specifically at the transition matrices and probability vectors of our process. Then, we will apply these matrices and vectors to develop the stationary distribution of the process. From there, we will evaluate the results of various Monopoly game simulations. This talk will provide a new lens with which to view a classic childhood board game.
Grant Pasterick - Network Graphs and Flow Algorithms, Advisor Dr. Danny Otero
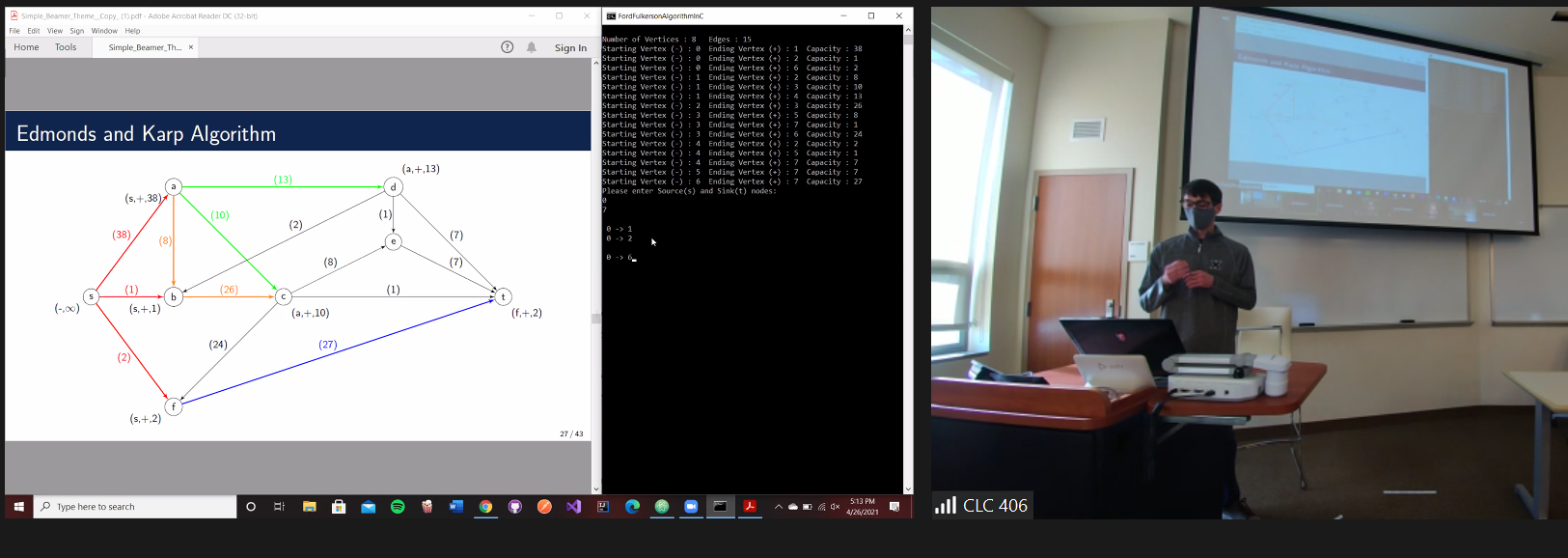
Graphs are helpful to describe networks of information, such as the movement of traffic, or data across the internet. The flow moving through these network graphs can be optimized through the use of different flow optimization algorithms. We examine in depth the Ford-Fulkerson and the Edmonds-Karp flow algorithm for network graphs and how their runtimes compare to one another.
Mark West - The Collatz Prime Problem: An Intractable Variant of an Intractable Problem, Advisor Dr. Danny Otero
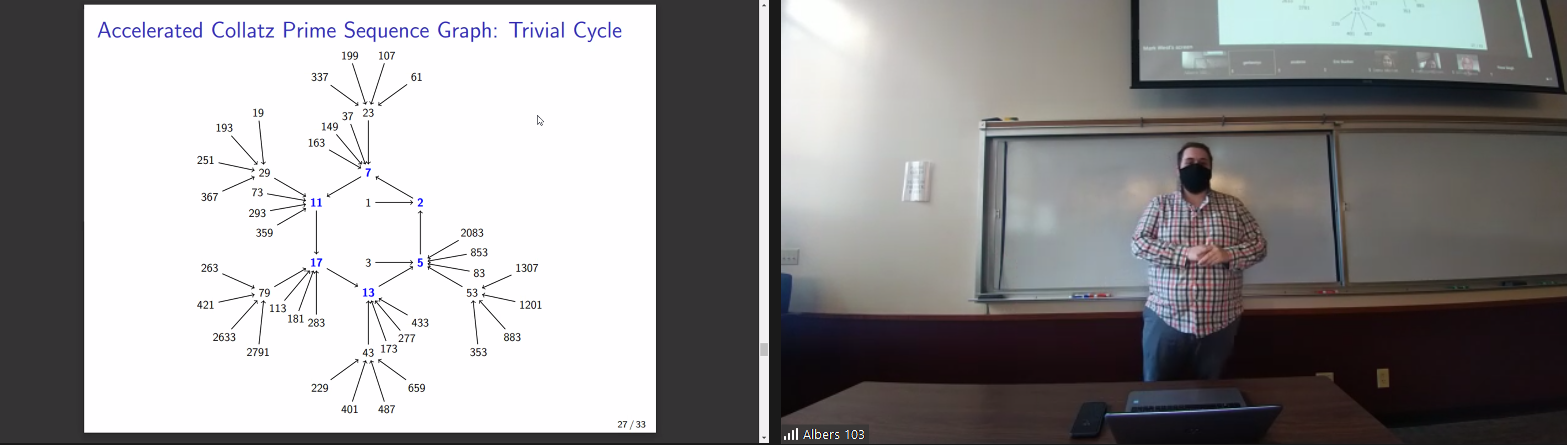
Take any positive integer; if it is odd then multiply it by three and add one, and if it is even then divide it by two. Repeat this process indefinitely and watch a pattern emerge. In fact, any number you begin with will result in the same pattern. At least, that is what is believed to be true, since no proof of this fact has ever been given. Lothar Collatz, a German applied mathematician, first formulated this problem in 1937 and it has carried his name ever since: The Collatz Problem. This problem is complex enough on its own, but what if we made it even more so? This project explores a unique variant of this problem involving prime numbers, producing a number of proofs and a few conjectures along the way.