Senior Projects 2019
Zach Almeida - Correlation between WAR and Rank in MLB, Advisor Dr. Grigory Sokolov

In this talk, we are going to determine if Wins Above Replacement (WAR) is related to the MVP winners in Major League Baseball. We will use results from the 2017 American League season along with the sample correlation coefficient as an estimator of the true correlation coefficient. The observed values of the sample correlation coefficient will be used as a function of Season and League (time) to examine dependency of the true correlation coefficient on time. Using a linear regression model, we will make predictions for the seasons that follow.
Daniel Bowling - The Number of Group and Ring Homomorphisms between Zm and Zn, Advisor Dr. Jim Snodgrass

In abstract algebra, we studied basics surround homomorphisms and particular examples of them between both groups and rings. In this talk, we will show the precise amount of homomorphisms between any two integer groups and rings with general modular constraints.
Kathleen Buch - Optimizing Congressional Districts Using a Genetic Algorithm, Advisor Dr. David Gerberry
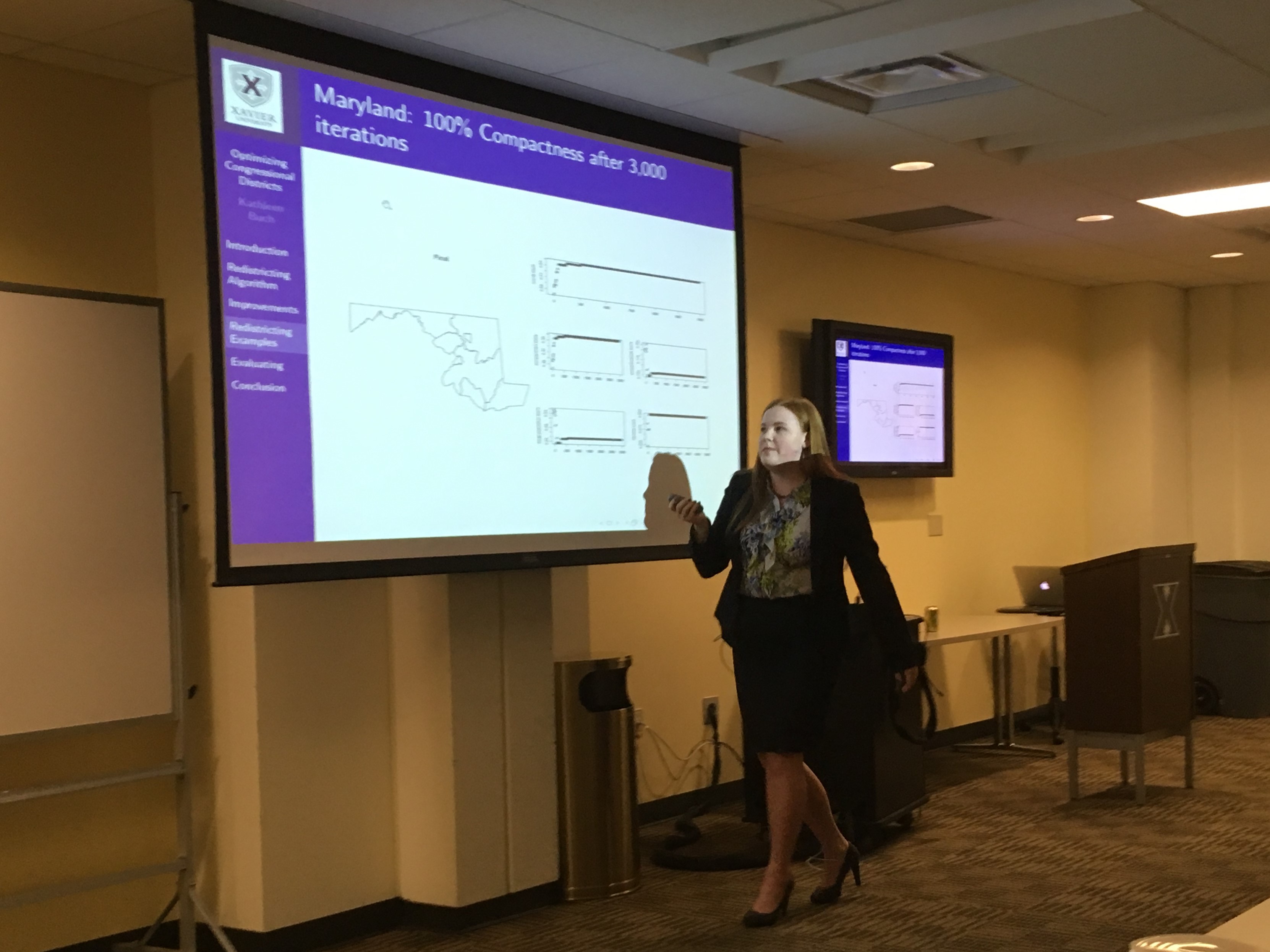
A continuation of an existing project that examines the existence of bias in the congressional redistricting process by creating an overall nonpartisan score for each district. The project has created a score based on, compactness, population equality, fairness, and competitiveness, that is used within an algorithm to mutate randomly generated districts. Recent improvements include cleaning and organizing existing code to create a streamlined process for generating districts for the use of further experiments and exploration. The project also introduces the idea and creation of Units. Breaking a state into Units stemmed from a recent law passed in Ohio that restricts the number of counties that can be split into different congressional districts. This mentality was used to create Units in Ohio and Maryland that have become the input to the algorithm. The project also addresses the relationship between fairness and competitiveness. Fairness aims to create congressional representation that is similar to the state popular vote. Competitiveness aims to make all districts a 50-50 Republican-Democrat split. It is suggested that these two are counterbalances for each other. Our simulation was run with varying weights for these two components to see if a negative relationship does exist between the two.
James Cerda - A Game of Labeled Chip-Firing, Advisor Dr. Eric Bucher

The world of mathematics is still very new when it comes to the Chip-Firing Game. In the few decades that this game was invented, many mystery and questions followed with it. Using several altercations to the original game, Labeled Chip-Firing will yield results that are fascinating.
Among Labeled Chip-Firing, we will go through the steps of how to play the game to better understand different moves, patterns of results and mathematical observations present. We will hear one theorem regarding one game scenario, as well as prove another theorem for a very different game scenario. Although we won’t discuss everything monitored, recorded, and noted in the process of this project, we will focus on a few interesting discoveries. The aim is to hopefully better your knowledge on the Chip-Firing Game, as well as encourage you to play the game yourself.
Jun Bum Cho -The Averch-Johnson Effect on the firm based on its type of industry and price for capital and labor, Advisor Dr. Hem Raj Joshi

The Averch-Johnson Effect states that a firm, whose objective is to maximize profit, would substitute labor for capital under a regulatory constraint. In general, the firm does not welcome a regulation because it causes a market inefficiency so that it hurts profit. The purpose of this paper is to examine if there are different effects based on the type of industry and price for the inputs. This paper shows that the Averch-Johnson Effect works in all cases besides the industries with a capital-heavy and relatively higher labor cost than capital and with a labor-heavy and relatively higher capital cost than labor cost. These two industries experience higher profits under the regulatory constraint.
Bryan Crigger - Quantifying the Madness of the Men's NCAA Basketball Tournament, Advisor Dr. Max Buot

The NCAA College Men’s Basketball Tournament, otherwise known as March Madness, is one of the most exciting annual sporting events in the United States. The unexpectedness, or “Madness”, of the single-elimination tournament draws millions of viewers around the world. Before it starts, many viewers fill out a bracket and essentially predict the results of the tournament. Despite the millions of brackets that are predicted each year, it is believed that no one has ever predicted March Madness perfectly: With a field of 64 teams competing in 63 total games, there are over 9.2 quintillion possible outcomes! In this project, we propose and examine various quantitative measures of Madness. We also attempt to address the following question: how can we reduce the number of likely bracket outcomes and increase our odds of correctly predicting who will win each game? By analyzing the levels of Madness that tournaments have had in past, we gain insight as to what may likely happen in future tournaments.
Rhea Elcock - A Comparative Analysis of Math Education: Singapore and the United States, Advisor Dr. Carla Gerberry

For the past decade, American students have been greatly out preformed in mathematics by Eastern Asian countries. In 2015, the TIMSS study tested mathematics achievement among 4th and 8th graders in various countries throughout the world. Its results showed, Singapore, Korea, Chinese Taipei, Hong Kong and Japan hold the top five seeds for student achievement in mathematics. For the United States, they stand 100 achievement points behind Singapore, at 11thplace. The question that arises then is, what are Eastern Asian countries doing in math education that the United States is not? Furthermore, how as a country can the U.S. improve its current state?
This project seeks to understand the history of math education in Singapore and the United States, while understanding its purpose in both countries. While looking at the current state of math education, this project also analyzes the four main differences between math education in both countries: national governmental control, framework and standards, mathematical content coverage, and stratification in math ability. Lastly while dissecting current pedagogy and comparing various math problems, this project establishes the strengths of America’s education system and yields possible improvements
Seth Hines - Examining the Friendship Theorem, Advisor Dr. Esmeralda Nastase
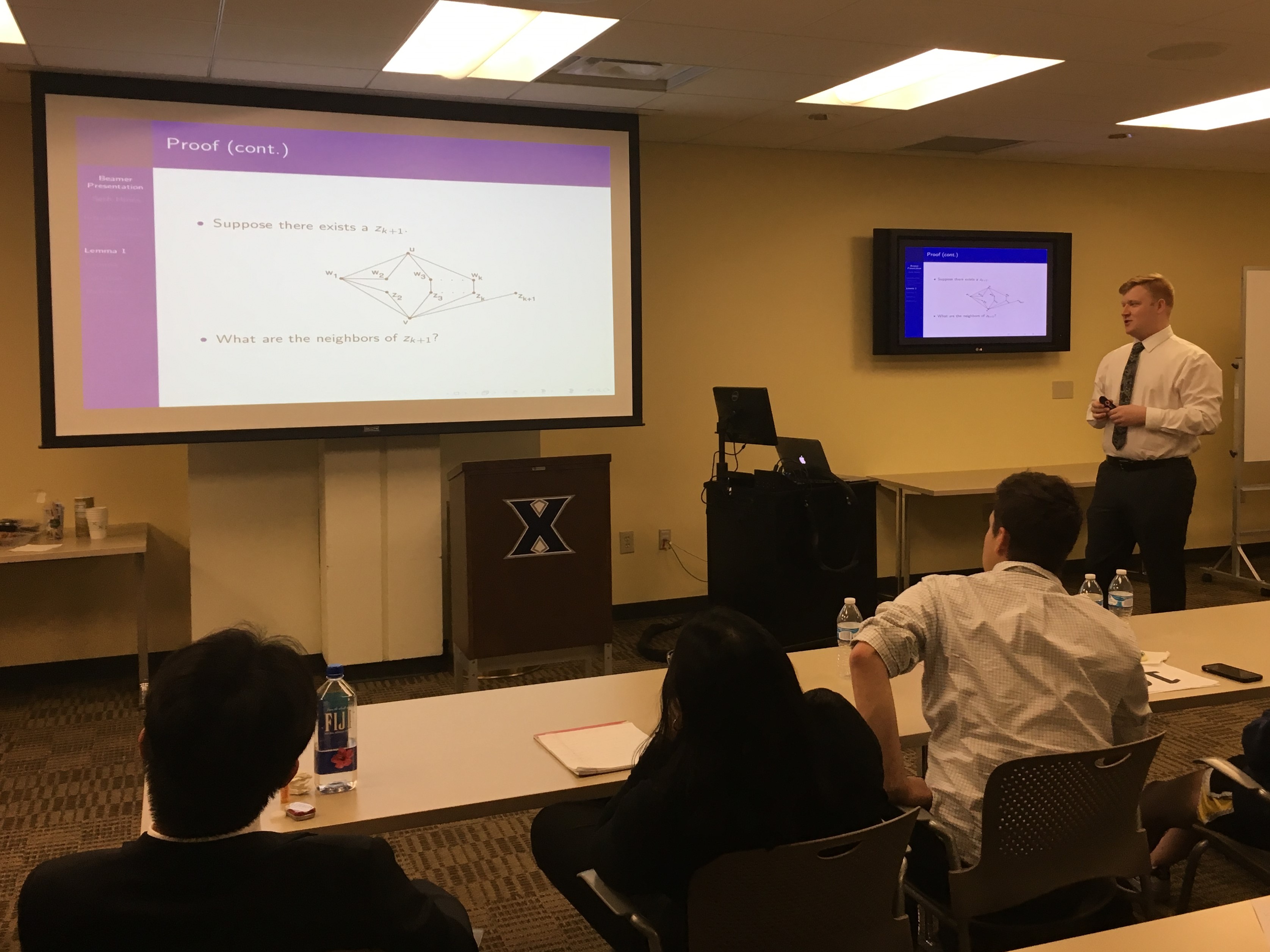
In this paper, we delve into the friendship theorem. This theorem uses graph theory to state, if we have a finite graph G in which any two vertices have precisely one common neighbor, then there is a vertex which is adjacent to all other vertices. We examine the proof to this theorem following a proof by contradiction along with two lemmas. The first lemma focuses on combinatorics while the second lemma applies linear algebra.
Brandon Luther - Nonparametric Statistical Inference and Count Regression Models, Advisor Dr. Roy Bower

In this talk, we analyze the results of two statistical analyses. We first seek to explore the use of nonparametric statistical tests with the median as measure of central tendency, in order to evaluate the use of biomarker MFAP4 as a predictor of hepatic fibrosis and cirrhosis in patients.
Second, in collaboration with the Xavier University Biology Department, we explore the relationship between types of lures and beetle attraction to the lures. Specifically, we focus on count regression model fitting and validation to confirm the beetles’ attraction to higher pheromone lures.
Annie McGhee - Motivations for STEM Teachers, Advisor Dr. Carla Gerberry

In recent years, there has been a deficit of qualified STEM teachers. In fact, according to a report to the National Council of Teachers of Mathematics, “only 41 percent of current mathematics teachers had mathematics as an area of study in college” (See Bibliography: Mitchell, 2005, p. 6). The motivations for and deterrents to becoming a STEM teacher must be analyzed in order to better understand the reasons for this shortage. Therefore, as an extension of research conducted in the summer of 2018 with Dr. Carla Gerberry, Dr. Mary Stroud, and Dr. Laura Edwards, I investigated motivations and deterrents of potential STEM teachers who had participated in the Breakthrough or Noyce internships. I performed qualitative analysis on twelve interviews to determine the possible intrinsic and extrinsic components that influence STEM students’ choice of profession, teaching or not. Preliminary results show that by highlighting the most rewarding elements of teaching and lessening the effects of potential disincentives, more qualified STEM teachers can be recruited and retained in the profession, aiding in addressing this deficit.
John Russell - The Application of Group Theory to the Rubik’s Cube, Advisor Dr. Jim Snodgrass

In this talk, we will focus on the Rubik’s Cube and the application of group theory. The question at hand is “How can we apply group theory within a mathematical toy, such as the Rubik’s Cube?” First, we will have a conversation about how the Rubik’s Cube came to be and its popularity. Second, we will apply group theory to the Rubik’s Cube to prove that it does indeed satisfy the properties of being a group. Finally, we will talk about God’s number, which is the maximum number of moves it takes to solve the Rubik’s Cube.
Katie Shannon - Modeling How Infectious Disease Generates Extreme Poverty Traps, Advisor Dr. David Gerberrry

This project explores how mathematics can be used to model how infectious disease can cause poverty traps in populations living in extreme poverty. An economic model and an infectious disease model will be explained individually followed by an exploration of the coupling of these two models. To end, various approaches to further changing and developing this model will be discussed.
December 2019
Garrett Lipps -The Financial Influence of Bayesian Probability, Advisor Dr. Grigory Sokolov

This research project poses the following question: how effective can a Bayesian model be when finding the probability that a stock's price will rise given the probability that the index price rises? Answering this question will allow the chance to develop a way of analyzing one of the most fundamental financial market pieces. People invest into stocks every day and this model will simply just be another attempt at forecasting the future events of stock and index prices. We will analyze the effectiveness of the proposed model on five real-life datasets and discuss how effective the Bayesian approach can be in the financial world.