Senior Projects 2017
Austin Fry - Can Mathematics Help End the Scourge of Political Gerrymandering? Advisor Dr. David Gerberry
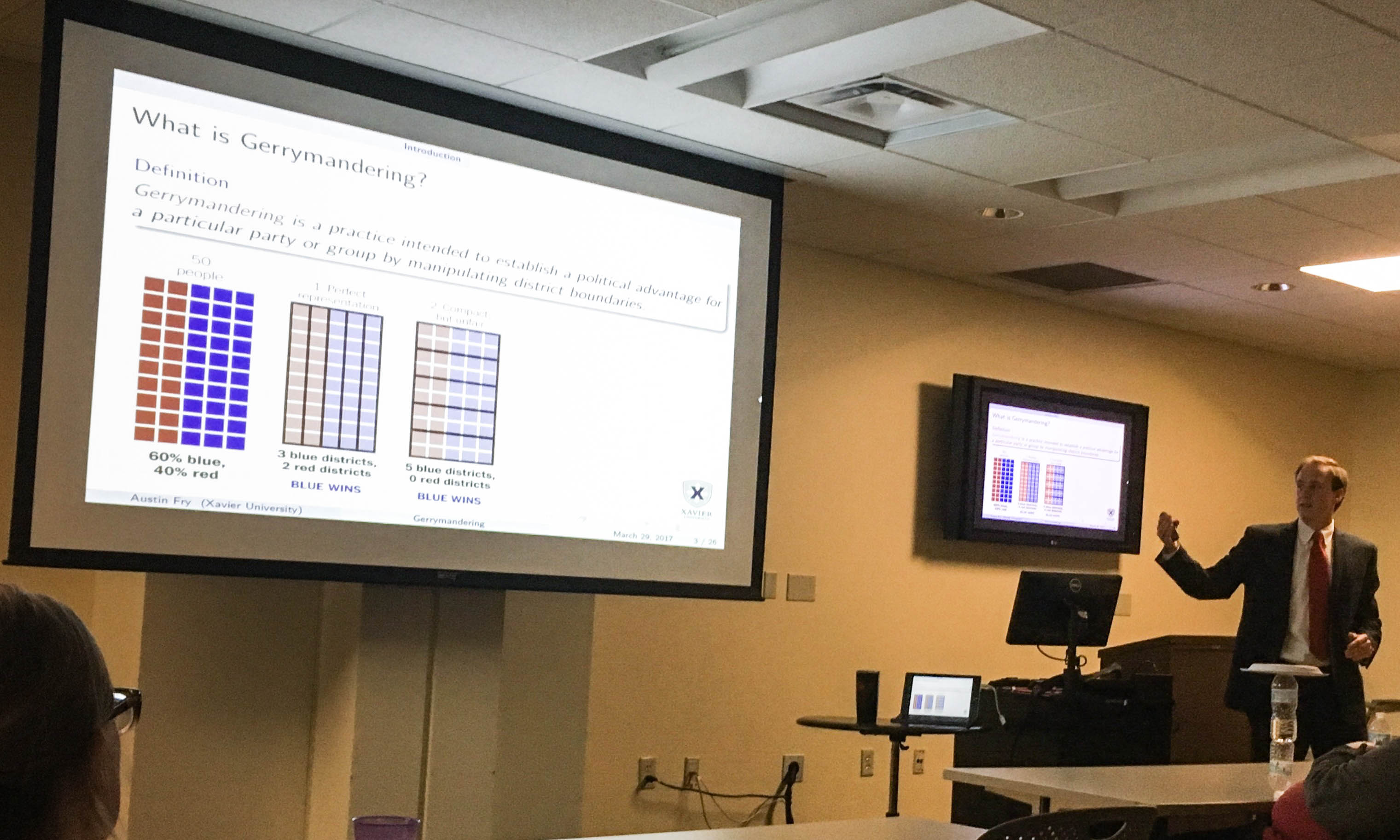
In recent years, Americans have become engrossed in politics. Unfortunately, the positive effect of having an engaged, informed electorate has been offset by the fact that political beliefs have become more polarized than ever. One of the main contributors to this polarization is the process of political gerrymandering where voting districts are drawn to favor a given political party. This leads to elected officials that are not representative of the political beliefs of a region and a larger number of noncompetitive voting districts. This lack of competition ultimately produces elected officials that are less willing to compromise.
In this research, we use a genetic algorithm approach to attack the Ohio Redistricting Competition created in 2009 to redraw Ohio Congressional districts. The competition rules judge the quality of a districting plan by 4 categories: compactness, communities of interest, competitiveness and representational fairness. Compactness assures bizarrely shaped legislature districts are minimized. Communities of interest give sense of place and shared interests among residents. Competitiveness allows the marketplace of ideas to be competitive and parties with a stronger voice choose their representatives. Representational fairness counterbalances competitiveness to assure a final redistricting plan does not unfairly bias one party over another. We have found that our genetic algorithm provides a particularly flexible framework for addressing the issue of political gerrymandering.
Casey Grubb - The Application of the Negative Hypergeometric Distribution to Russian Roulette, Advisor Dr. Max Buot
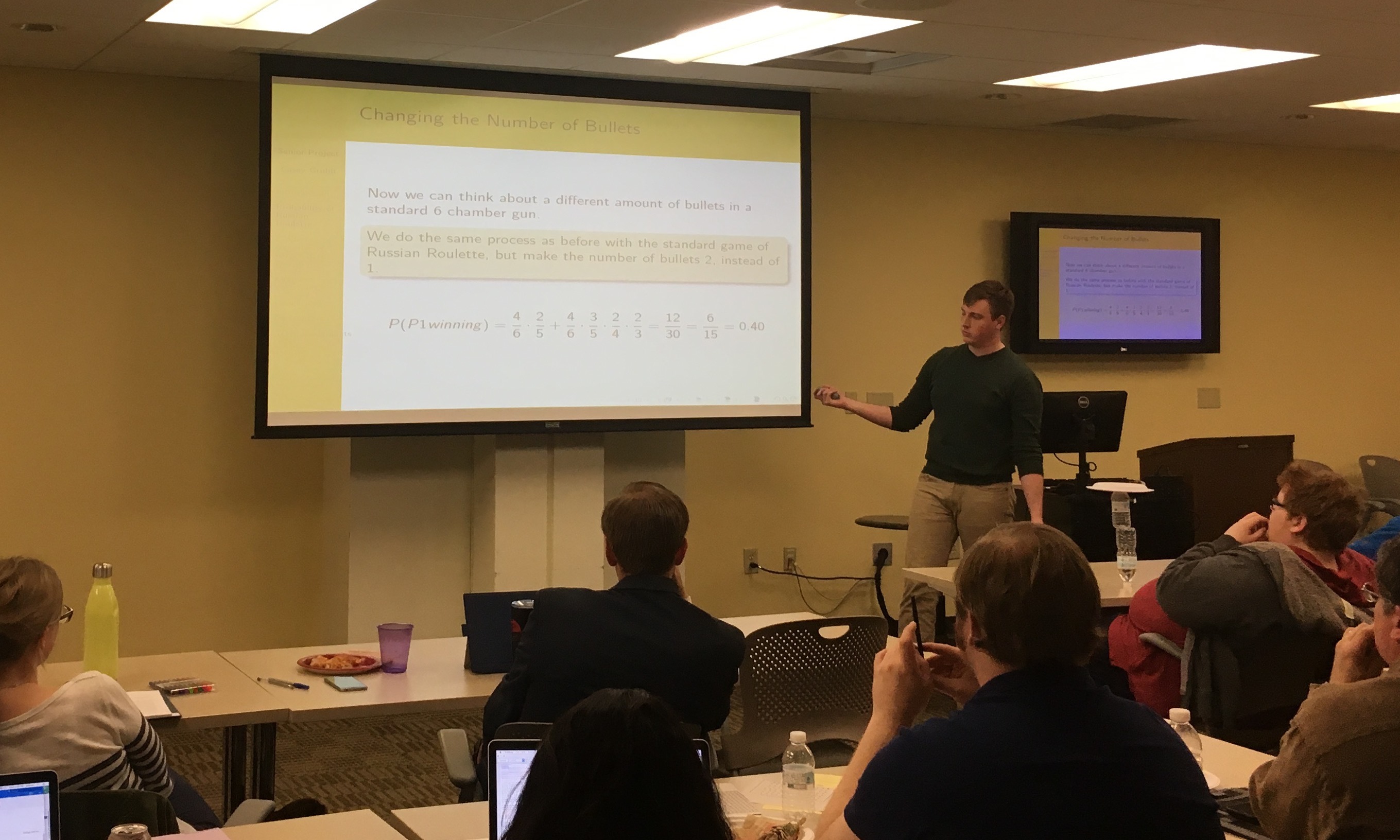
Suppose two opponents play the high stakes game of Russian Roulette. Does it matter which player goes first, or is Russian Roulette a fair game? In this project, we study the Negative Hypergeometric probability distribution, and demonstrate how it can be used to model Russian Roulette. We analytically derive the probabilities of the first player winning, and find conditions in which the game is fair. Moreover, by modifying the parameters of the Negative Hypergeometric probability distribution, we calculate winning probabilities for different variations of "classical" Russian Roulette. For some variations, we create a simulation in the R programming language to estimate the probabilities of the first player winning. For example, in the game of "Egg Russian Roulette" played on the Tonight Show with Jimmy Fallon, we find that the first player (who is usually a celebrity guest) has a 45% chance of winning the game!
Sebastian Hoar - Improving on Least Squares Regression with Lasso Constraints and Convex Optimization, Advisor Dr. Max Buot
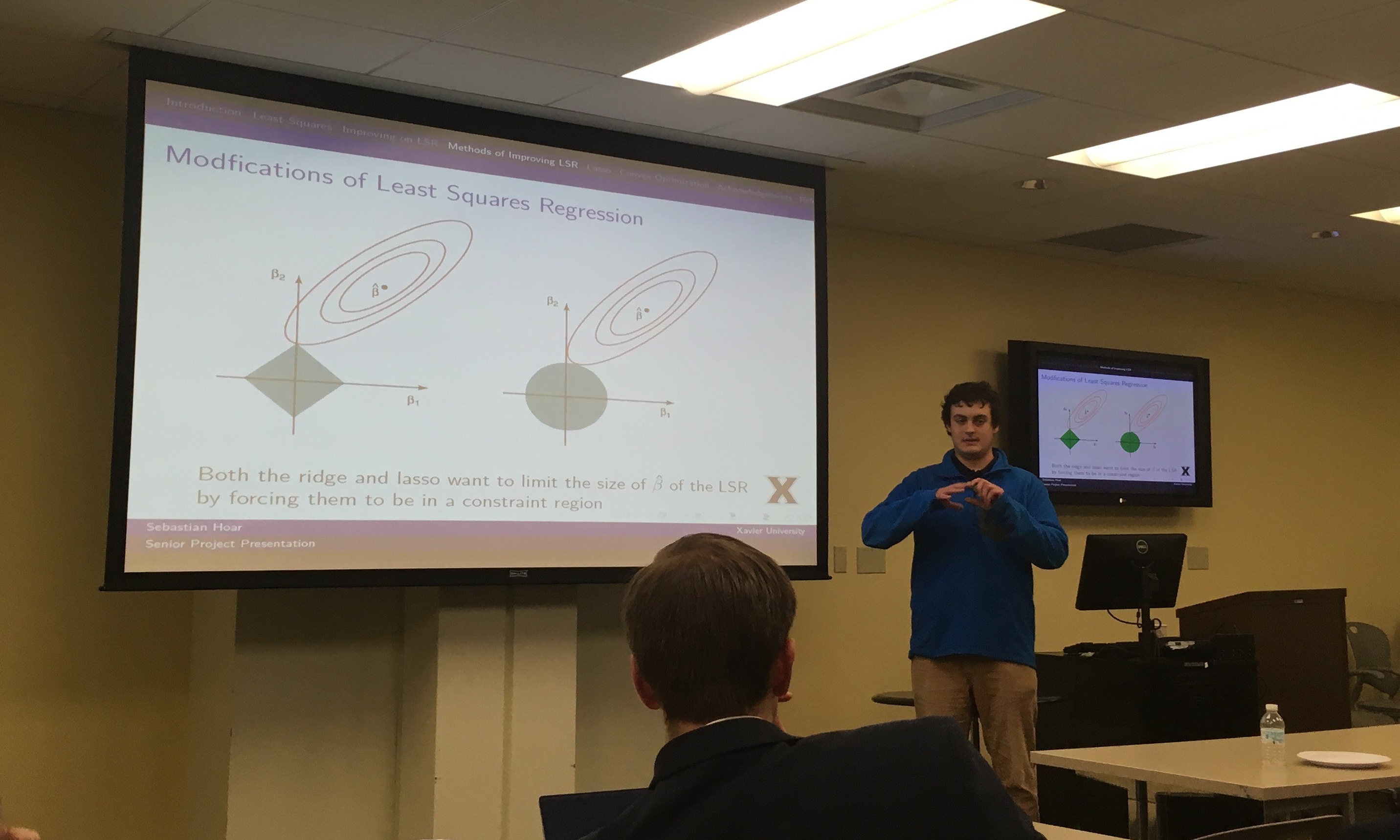
Least squares regression is a simple but powerful method for modeling and predicting the relationship between two numerical variables. The parameters of the model are found by minimizing the sum of squared residuals between the predicted observations and the actual observations. However, even assuming a linear underlying relationship, least squares regression has some limitations. For example, if the number of predictor variables is large, then the model may overfit the data, and result in a high mean squared error of the predictions. Also, if the number of predictor variables is larger than the number of observations in the data set, then some parameter estimates will have infinite standard errors. This paper looks at how the "lasso" (least absolute shrinkage and selection operator) addresses these issues. We also demonstrate convex optimization methods to estimate the parameters of the lasso regression model.
Veronica Lawrence - The Dinitz Problem, Advisor Dr. Esmeralda Nastase

The Dinitz Problem is a graph theoretical coloring problem raised by Jeff Dinitz in 1978. The Dinitz problem asks if it is always possible to color each (i; j) cell of an n x n Latin Square with a color from the set C(i; j), in such a way that colors in each row and each column are distinct. In this paper I explore the graph theoretical approach and solution published by Fred Galvin in 1993. In doing so I will give in depth explanations of any graph theoretical concepts used, giving proofs where appropriate. After exploring Galvin's solution I will explore Jeannette Janssen's proof of the Dinitz Problem applied to Latin rectangles. Finally, I will detail the connection between the results of both Galvin and Janssen to the list-chromatic number of hypergraphs.
Abby Moninghoff - A Look into Non-Standard Analysis with Torricelli's Trumpet and Roberval's Cycloid, Advisor Dr. Danny Otero

The calculus we study as math majors that was developed by Newton and Leibniz requires the use of derivatives and integrals that stem from our standard analysis and rigorous application of calculus. This rigorous approach was introduced by Weierstrass when he formalized the definition of a limit using e-d in the 1870's. In my paper, I examine how 17th century mathematicians such as Torricelli and Roberval used infinitesimals and indivisibles to solve problems we often find in modern calculus textbooks. This intuitive approach to the calculus relies on non-standard analysis and first requires the creation of the hyperreal numbers from the real numbers.
Drew Philip - The Effect of the Incidence Function on the Existence of Backward Bifurcation, Advisor Dr. David Gerberry

In modeling the dynamics of infectious disease, the choice of the specific mathematical formulation of disease transmission (i.e. the incidence function) is one of the initial assumptions to be made. While inconsequential in many situations, we show that the incidence function can have an effect on the existence of backward bifurcation (the phenomenon where a disease can persist even when the basic reproductive number is less than 1). More specifically, we compare mass action and standard incidence (the most common incidence functions) versions of two hallmark models in the backward bifurcation literature and an original combination model. Our findings indicate that the standard incidence formulation of disease transmission is more conducive to backward bifurcation than mass action, a trend seen in all the models analyzed.
Matthew Suggs - Getting to Third Base (or is it base 3?) with the Cantor Set, Advisor Dr. Jim Snodgrass

The Cantor Set C is the set of numbers obtained by removing the open middle third (1/3, 2/3) from the closed interval [0, 1] and then iterating this process ad infinitum. To derive some of the properties of C it is helpful to express its points in ternary notation. Having done this we can easily show that C is uncountable. C also has a number of interesting topological properties. It is closed, compact, dense-in-itself, nowhere dense in [0, 1], and satisfies the separation axioms T0, T1, T2, T3, T4, and T5.
Becky Wandishin - An Analysis of the Enigma Machine, Advisor Dr. Dena Morton

In this paper, I examine the two main Enigma cryptographic machines used during World War II: the Wehrmacht and the Kriegsmarine M4. In this examination, I look into a brief history of the utilization and cryptanalysis of these machines. An in-depth explanation and analysis of the various parts and overall connections of these parts is also conducted. I evaluate the total possible number of combinations that could have been used if the Nazi regime had utilized these machines to their fullest extents, and then compare that number to the actual use during the war. Finally, I perform a proof showing that no letter could be encrypted to itself, which was the major flaw in the Enigma, and which allowed the Allies a path into breaking the Enigma machine.